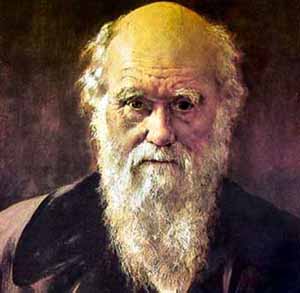
EECS 492 A1 Results

EECS 492 A1 Results
Christopher Spencer Buja
September 25, 2015

A1 Results

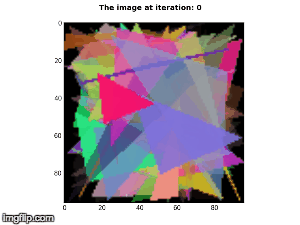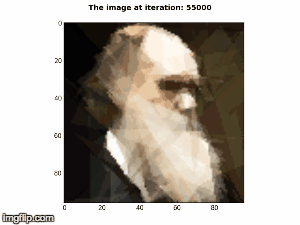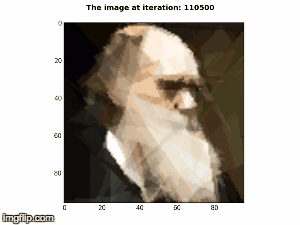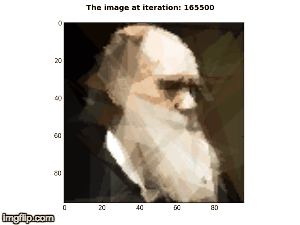
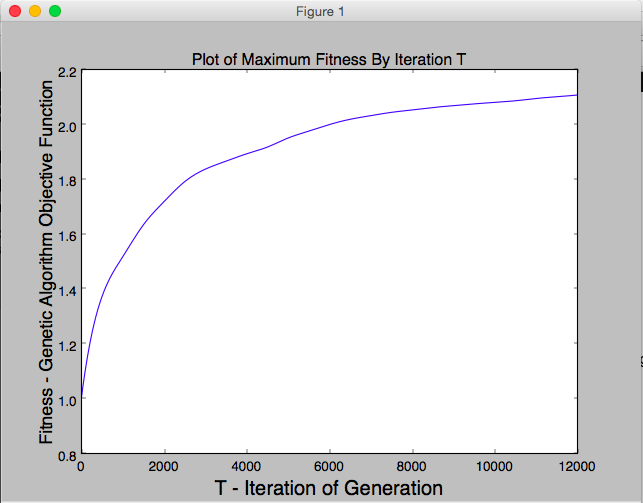
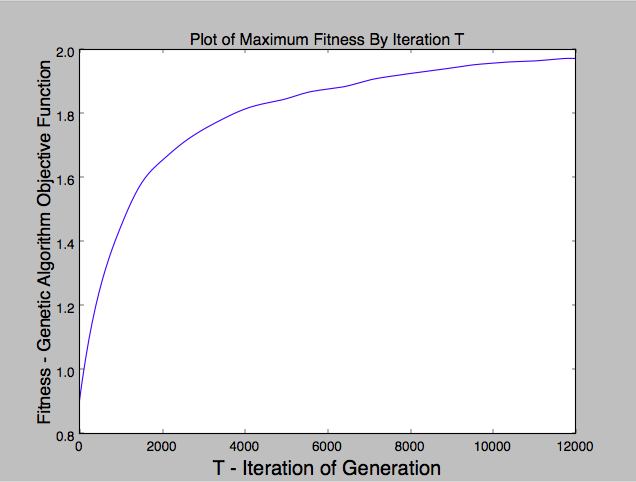
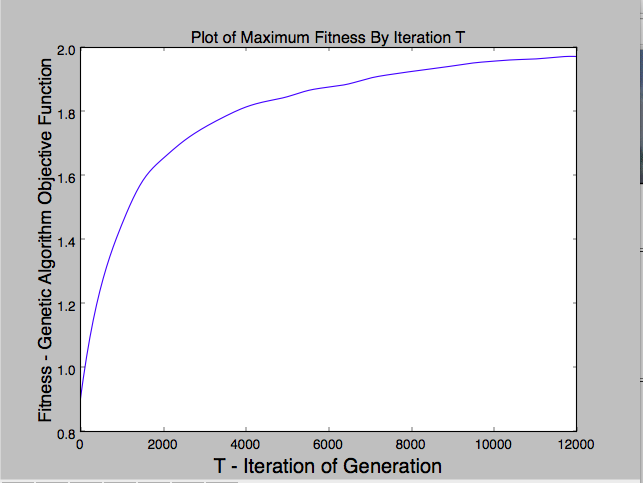
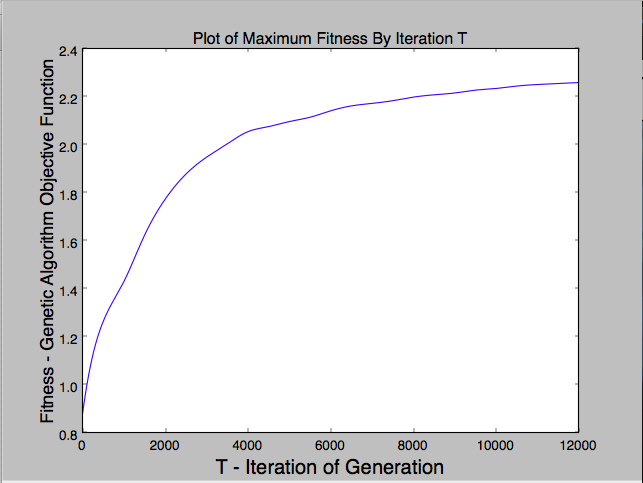
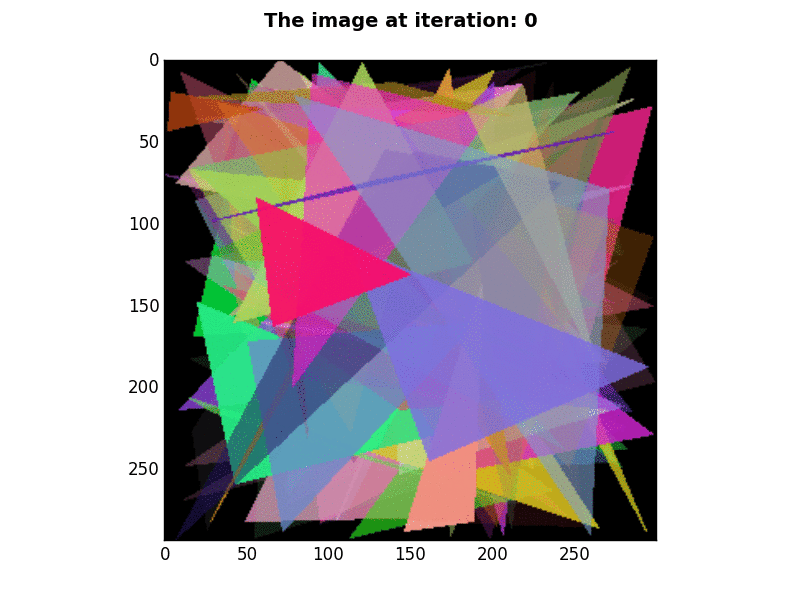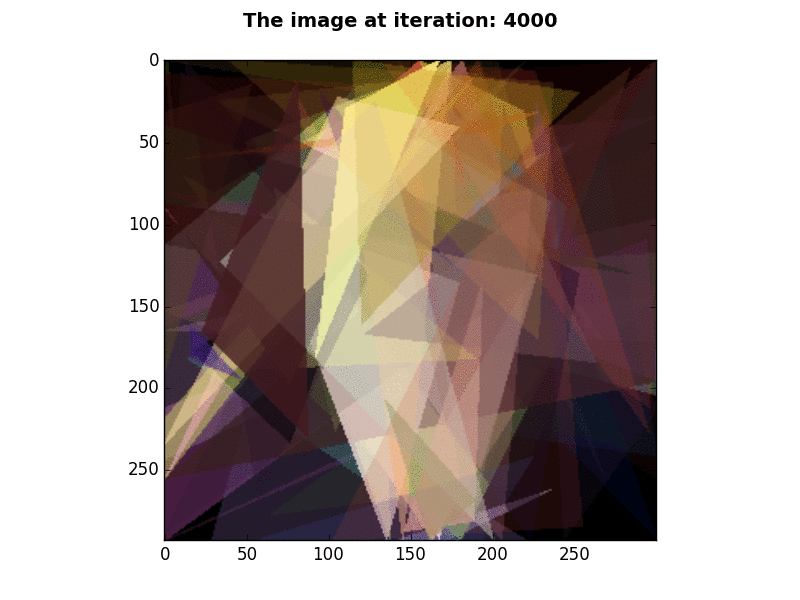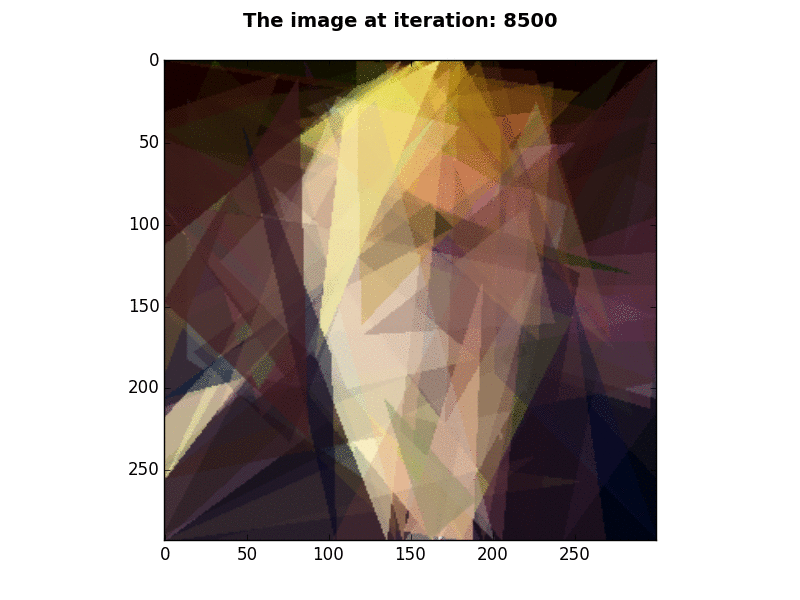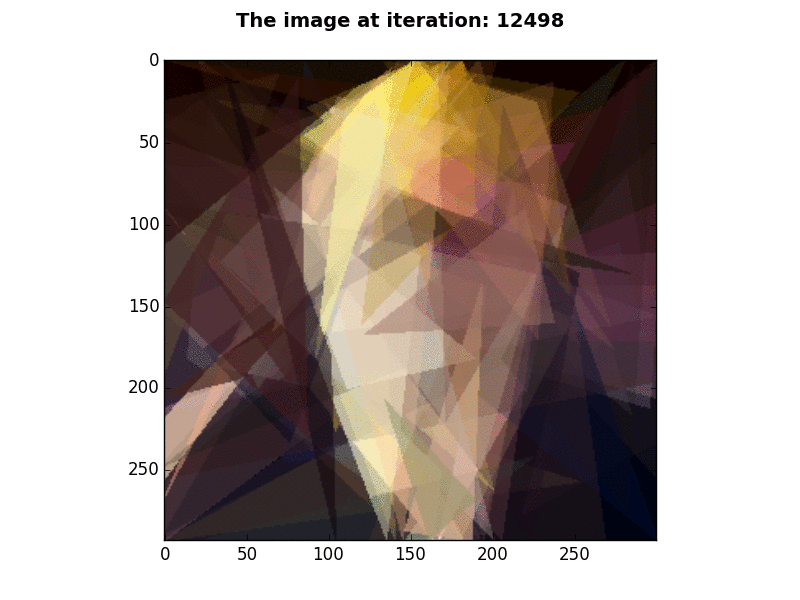
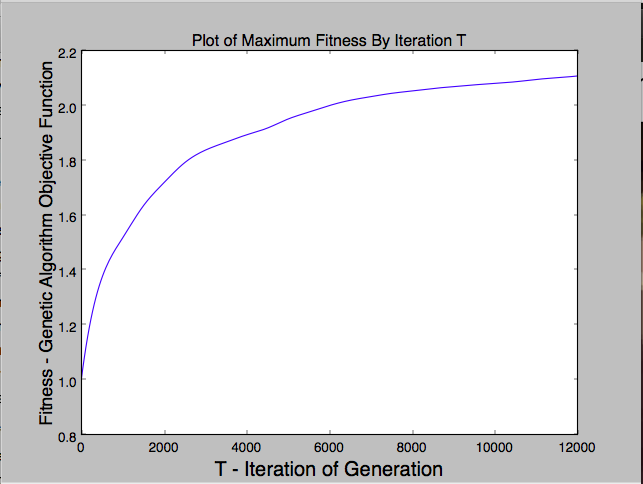
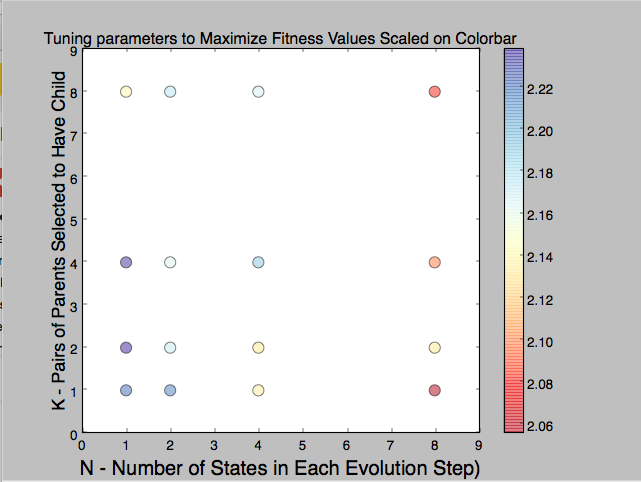
The purpose of this project is to recreate Roger Alsing's work on genetic programming to create art. The population consists of approximations to a given image. Each image uses P polygons, where P=100 for the results on this page. N is the population size and K is the number of new children created per generation. T is the number of generations displayed in each animation. The fitness of the image is a measure of how closely it matches the original image. The learning curve shows how the fitness of the best approximation improves over time. The 2D graphs depict how the fitness after T generations varies with N and K where the color of the points on the graph scale with the best fitness score obtained with parameters N and K.

Original image	Approximation	Learning curve
96×96 pixels	P=100, N=1, K=2, E=331001
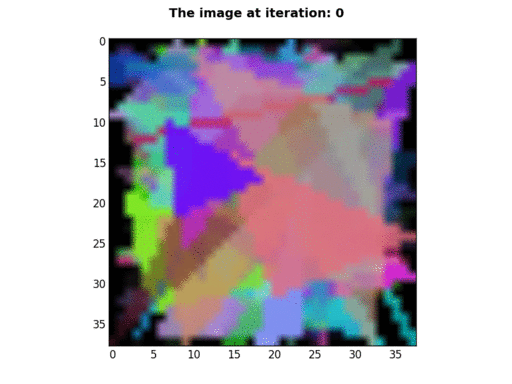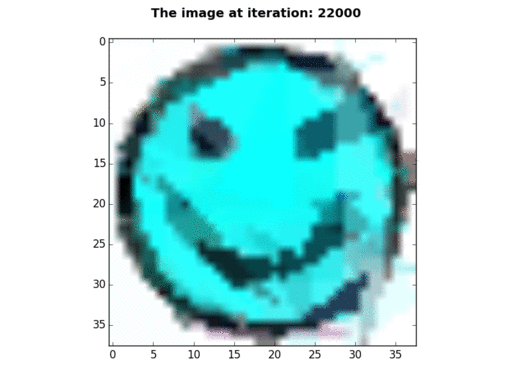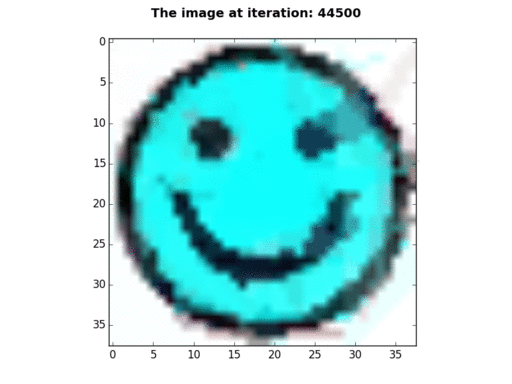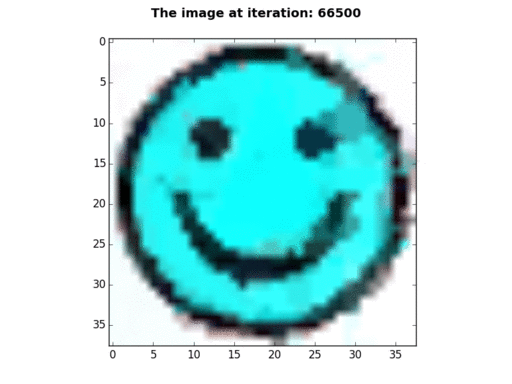
38×38 pixels	P=100, N=1, K=2, E=133001 - This gif was created by displaying BGR values, instead of RGB values.
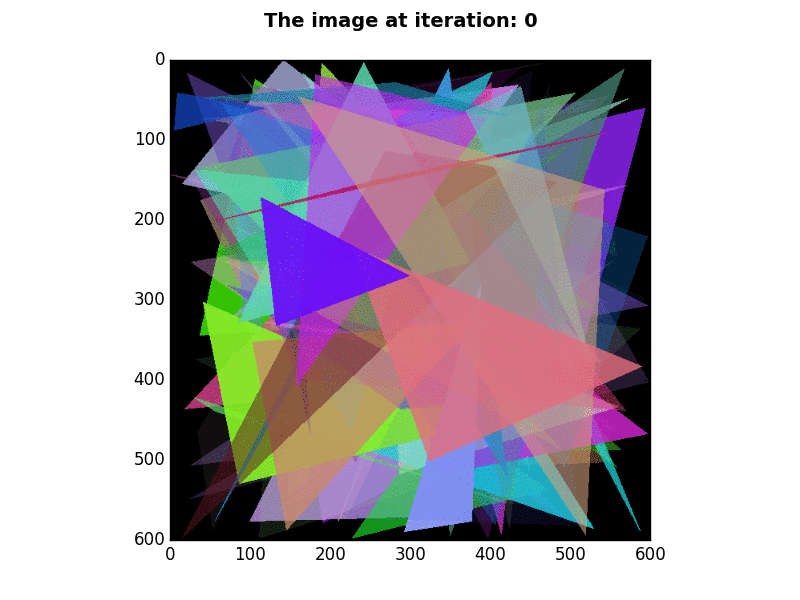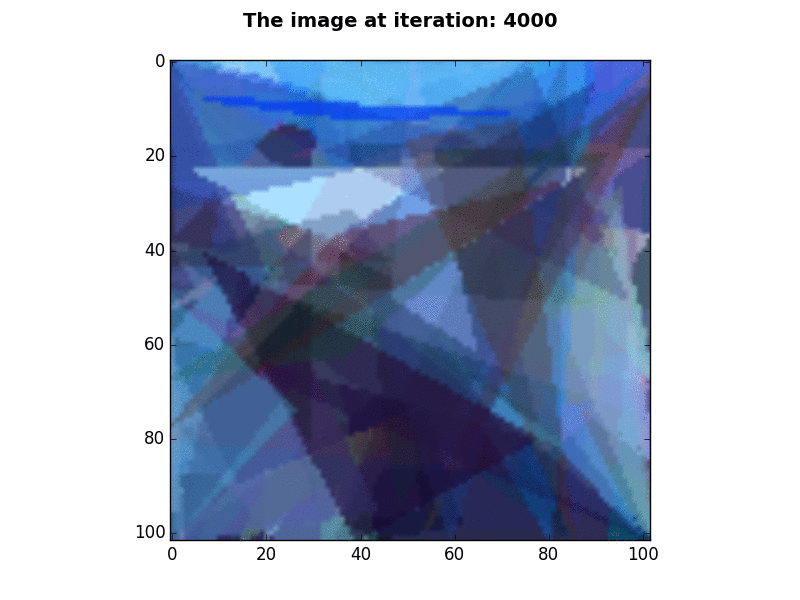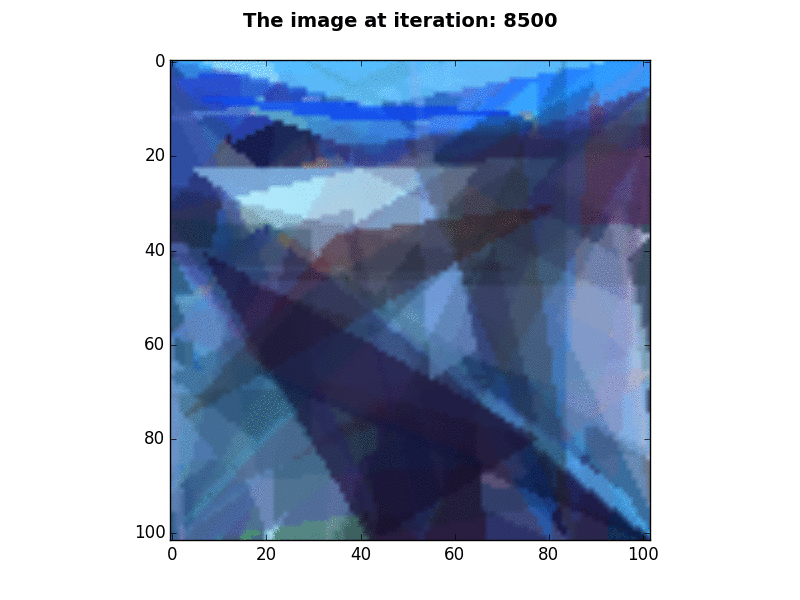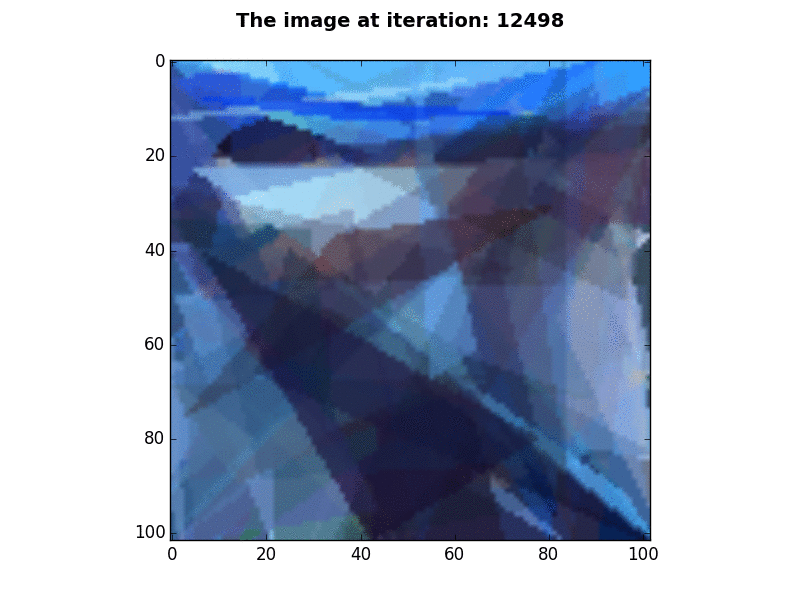
102×102 pixels	P=100, N=1, K=2, E=25,000 - This gif was created by displaying BGR values, instead of RGB values.
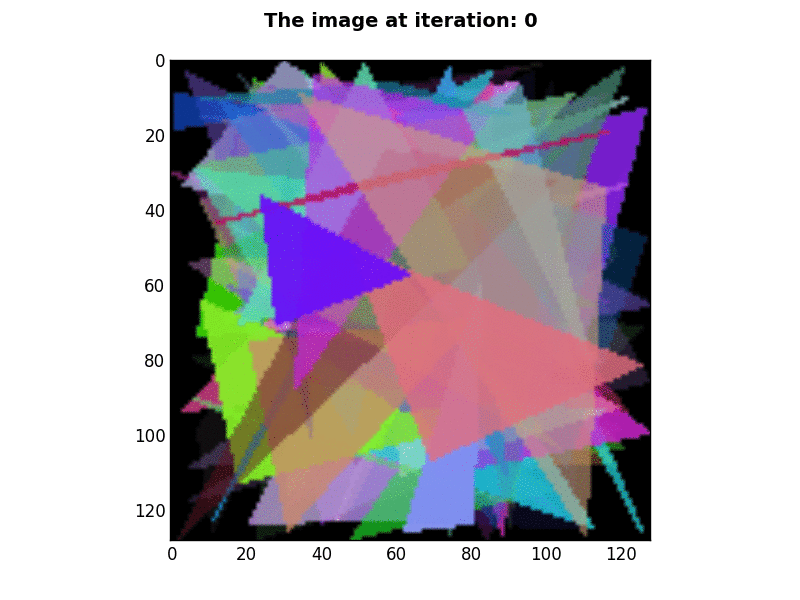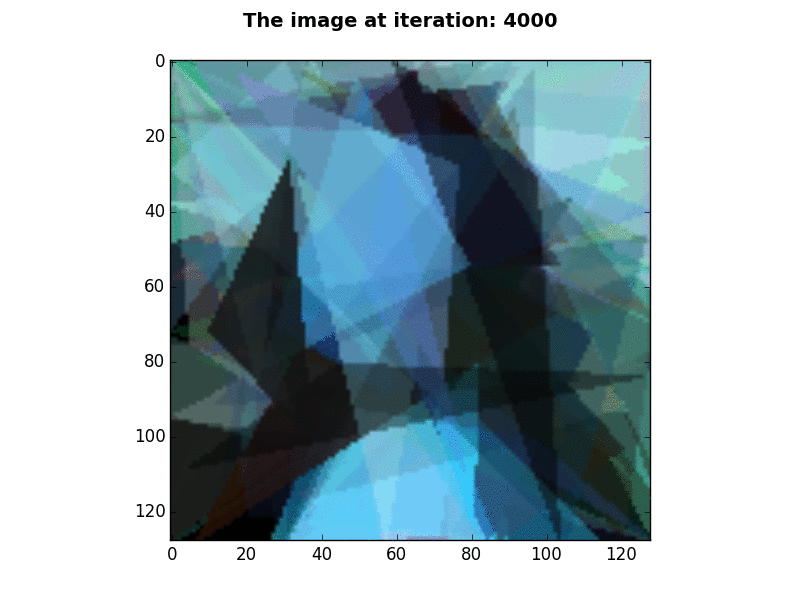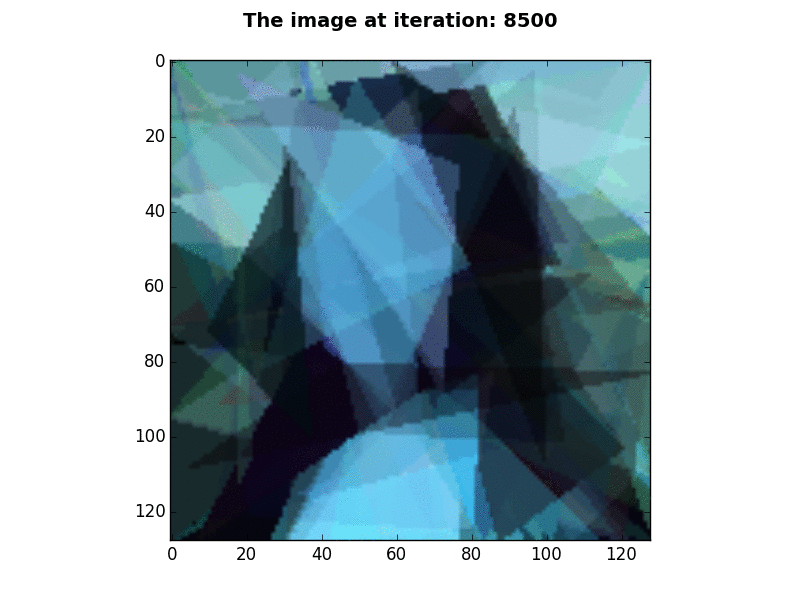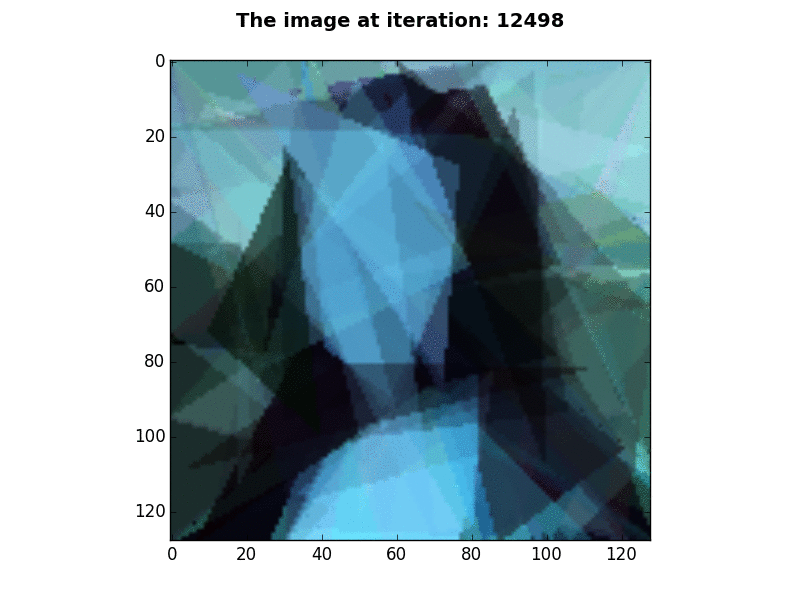
128×128 pixels	P=100, N=1, K=2, E=25,000 - This gif was created by displaying BGR values, instead of RGB values.
300×293 pixels	P=100, N=1, K=2, E=25,000

I searched to find the best parameters to get the highest fitness value. N=1, K=2 gave the best result overall after 25000 generations. This I applied the genetic algorithm for the purposes of this graph on the small darwin image at the top.

Mutations for a child generated from crossover:

With 1/4 probability, slightly change position of all points in a random polygon.
With 1/4 probability, slightly change the alpha value of random shape.
With 1/4 probability, slightly change all three rgb values of a random polygon.
With 1/4 probability, change the render ordering of two polygons.

Coordinates of vertices were moved using a Gaussian distribution where the mean is the previous coordinate, and the variance is 0.2 multiplied by the maximum width or the height.
RGB values (0.0 to 255) were altered using a Gaussian distribution where the mean is the color, and the variance is 40.
Alpha values were altered using a Gaussian distribution where the mean is the former alpha value, and the variance is 0.2 .
Ordering was changed by drawing from a discretized uniform distribution twice and changing the rendering order of the polygons.

Random triangles were created by picking three points on the image with uniform distribution, and filling the area between those points with an rgb and alpha value.

Parents were selected using the roulette selection algorithm. This made the more fit individuals more likely to be chosen for crossover.